Sonnenspektrograph
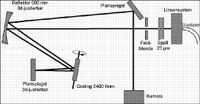
Unsere neueste Entwicklung ist ein Littrow-Spektrograph hoher Auflösung (größer als 100.000) mittels zweifacher Gitterdispersion und langbrennweitigem Hohlspiegel.
Abb. 1: Strahlengang des Sonnenspektrographen
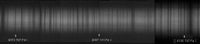
Abb. 2: Originalaufnahmen mit einer einfachen WebCam und sense-up Technologie.
Abbildung 2 zeigt einen Ausschnitt des Sonnenspektrums bei 6300 Angström mit einer spektralen Gegenüberstellung des westlichen und östlichen Randes am Sonnenäquator. Bei einer äquatorialen Drehgeschwindigkeit von 2 km/s kommt es am Westrand zu einer geringfügigen Rot- und am Ostrand zu einer Blauverschiebung der Absorptionslinien. Als Referenz dienen die atmosphärischen Sauerstofflinien, deren Positionen unverändert bleiben (Balthasar 1982). Ihnen gegenüber sind die Eisenlinien am Westrand ins Rote und am Ostrand ins Blaue verschoben. Diese Verschiebung beträgt (um 6000 Angström) jeweils lediglich 0,04 Angström, was zu einem Versatz von 0,08 Angström der Eisenlinien zwischen West und Ost führt. Dieser geringfügige Unterschied läßt sich mit dem neuen Spektrographen eindrucksvoll demonstrieren.
Die Wellenlängenangaben sind der Second Revision of Rowland's Preliminary Table of Solar Wavelengths Monograph 61 National Bureau of Standards 1966 ( 2. RRT ) entnommen. Sonnenspektren in diversen Auflösungen gibt es hier und incl. Sonnenflecken hier.
Das Sonnenspektrum von 3900 bis 6900 Ångström
Aufgenommen mit einer Mini Square Camera JMF-N511W (1/3" Sony ICX811 Chip in Schwarz-Weiß-Einstellung) mit Sense-Up-Technologie von Variovision. Der Vergleich mit einer besseren Kamera (Watec 120N etwa) zeigt die Probleme auf, welche man bekommt, wenn mit teuren Kameras gearbeitet wird. Diese verfügen (wie auch normale Webcams) über Deckgläser vor dem Chip, die einerseits als Schutz dienen, andererseits aber auch UV und IR abblocken - aber kaum entfernbar sind. Der geringe Luftspalt zwischen diesen Abdeckungen und dem Chip führt zu "Interferenzen an dünnen Schichten", die bei Ölfilmen "Newton'sche Ringe" genannt werden und in Fabry-Perot-Anordnungen sogar gewollt sind; und bei Hochauflösungen bilden sie unvermeidbare Schrägstreifen, wie unten deutlich zu sehen ist. Diese Interferenzen werden um so ausgeprägter je monochromatischer (entsprechend hochauflösender) das Strahlenbündel wird.
Bild 3:
Bei den Profis in den Großsternwarten werden diese Mehrfachinterferenzen (auch Fringes genannt) durch Einbringung keilförmig geschliffener Gläser entfernt. Diese äußerst kostspielige Vorgehensweise ist für derartige Klientel kein Problem, da ihre Finanzierung durch die öffentliche Hand (Universitäten und nationale sowie internationale Institute) und nicht aus privaten Schatullen erfolgt.
Bei den billigen Webcams kann man als Amateur mit angemessener Vorsicht die Blockfilter entfernen und vermeidet somit diese Störungen. UV und IR führen nicht zu Bildverschlechterungen, da beide im spektralen Modus ausgeblendet werden.
Gewiß, gewiß !!! Im Gegensatz zu teuren Kameras sind mit dieser "Sparversion" zunächst nur sehr unsichere Analysen (bis zu 50% Unsicherheit) der Äquivalentbreiten und Flügelstärken von Linien möglich. Die Ermittlung der Apparatefunktion (van de Hulst 1941) zur entsprechenden Korrektur der Linienprofile ist kompliziert, denn die verwendete Kamera (Gamma-Einstellung 0,20) hat beileibe keine lineare Schwärzungskurve und die Einkopplung des Sonnenlichtes erfolgte durch einen 6 Meter langen Lichtleiter. Beides zusammen verfälscht die Kontraste der Linienkonturen und macht die Komplexität einer entsprechenden Korrektur aus.
Eine erste Annäherung zum tatsächlichen Profil der Absorptionslinien erhält man infolge einer Anhebung des Kontrastes durch Gamma-Korrektur mit 1,25 (Software ImageJ).
Mit kostenlosen (Iris und VisualSpec) und kostenpflichtigen Programmen (https://rspec-astro.com) lassen sich dann auch eindimensionale Absorptionsspektren generieren. Sie verlangen Fits-Spektren, die mit der Konversionssoftware Spesoft erstellt werden können.
Untersuchungen zum Apparateprofil mit Graukeilen und -filtern bekannter Schwärzung sind im Gange und werden auch hier veröffentlicht werden.
Auf den Kamerachip entfallen ca. 8 Ångström - im Blauen mehr, im Roten weniger - und die Spektralstreifen von 25 Å sind durch Überlappung zusammengesetzt. Öfter führt dieses Verfahren zu Helligkeitschwankungen des Kontinuums. Wellenlängen sind der oben angeführten Rowland-Tabelle (2.RRT) entnommen.
(Einfachklick auf die Miniaturansichten führt zur vollen Auflösung.)
Eine Zusammenstellung als pdf-Datei gibt es hier.
Nachfolgend ein Beispiel für die Brauchbarkeit der Spektren zur Bestimmung der Äquivalentbreiten (EW) und Flügelstärken von Absorptionsprofilen. Für erstere entnehmen wir Daten aus einer Arbeit von Mulders 1935 (Seite 302) und vergleichen sie mit Rechnungen, die aus den Anwendungen von Vspec und Rspec gewonnen werden. Da Rspec die EW nur mit zwei Stellen hinter dem Komma angibt, haben wir hier die Kalibrierung der Wellenlängenskalen mit dem Faktor 10 versehen (also 55657,15 Ångström statt 5565,715; die sich daraus ergebenden EW-Werte wieder durch 10 dividiert führt zu den gängigen dreistelligen Milli-Ångström).
Wir beschränken uns auf EW-Werte bis 500 mÅ, denn bei den starken Linien (etwa H und K von CaII, Magnesium-Triplett, Na-Dublett, Balmerlinien sowie starken Eisenlinien wie etwa bei 4404,761 Å) wird es mit der Extrapolation zum Kontinuum und der Löschung überlagernder Linien sehr schwierig und führt zu erheblichen Unterschätzungen.
In nachfolgender Tabelle 1 sind alle Äquivalentbreiten zusammengefasst. Die Wellenlängen sind gegenüber Mulders der 2.RRT angepasst (lediglich Änderungen an der dritten Kommastelle).
Tabelle 1: Äquivalentbreiten
Gegenüberstellung von Vspec und Rspec
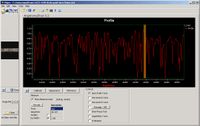
Abb. 4: Vspec Spektroskopie Programm
Abb 5: Rspec Spektroskopie Programm mit Faktor 10 erweiterten Wellenlängen
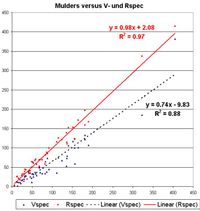
Abb. 6: Lineare Korrelation der Äquivalentbreiten - Abszisse Mulders, Ordinate Vspec resp. Rspec(rot).
Die Graphik macht deutlich, dass mit Rspec eine bedeutend bessere lineare Korrelation (Bestimmtheitsgrad und Korrelation fast gleich 1) als bei Vspec erreicht wird.
Die Bedeutung von Flügelstärken liegt in der Analyse des Gasdruckes von Sternatmosphären (der Begriff Flügelstärke wurde von Voigt 1949 eingeführt, von Weidemann 1954 und von van't Veer 1961) und ihrer Beziehung zur Äquivalentbreite (Minnaert 1935, Seite 50). Zur Berechnung von Flügelstärken nehmen wir als Beispiel die Na-D2-Linie. Nach einer Gamma-Korrektur der originalen CCD-Aufnahme von 1,25 und der Übertragung eines Spektralstreifens entlang der D2-Linie in eine Excel-Matrix mittels Vspec kommen wir nach einigen Rechnungen zu folgendem Ergebnis:
Abb. 7: Linienprofil der Natrium D Linie
Abb. 8: blauer Flügel
Abb. 9: roter Flügel
Bezüglich der Details zur Ermittlung von Flügelstärken sei auf die Arbeiten von Minnaert 1935, Houtgast 1942, Priester 1953 und die "Bibel" der Sternphysik von Unsöld (Physik der Sternatmosphären 1955, Seiten 245 und 448) verwiesen. Für die Natrium D2-Linie sind dort (Minnaert, Seite 50, Houtgast Seite 69 und Priester, Seite 246) C-Werte um 0,09 angegeben, was mit unseren 0,09 des blauen Flügels übereinstimmt. Die Unsymmetrie der Linie führt bei uns zu einem geringeren Wert (0,06) im roten Flügel.
Damit ist der Einsatz obiger Spektren für analytische Zwecke zufriedenstellend und zunächst überraschend angesichts der Tatsache, dass sie mit einer Webkamera zustande kamen.